Ormai da quasi due anni ci sentiamo ripetere che le scelte politiche e, di conseguenza, le nostre vite dipendono dalle previsioni del Comitato Tecnico Scientifico. Ma cosa vuol dire prevedere? Cosa fanno nella pratica lɜ scienziatɜ per guidare le scelte politiche? Sono per caso espertɜ fattucchierɜ che leggono il futuro nelle sfere di cristallo?
Purtroppo per noi, nessuno scienziato è un mago. Tendenzialmente sono fisicɜ, matematicɜ o informaticɜ (o un mix di tutti questi) che cercano di creare modelli che possono ben descrivere i dati e provare a prevedere sviluppi futuri di un fenomeno. I modelli non sono altro che strutture che vengono prodotte trasformando le informazioni che abbiamo dalla realtà in oggetti matematici, messi in comunicazione tra di loro attraverso equazioni e formule. Si parte sempre da una semplificazione anche estrema della realtà, per cercare di capire quali siano gli elementi che maggiormente influenzano il fenomeno studiato.
Quello che fa la cosiddetta Fisica dei Sistemi Complessi, è applicare questi modelli matematici alla realtà e provare a risolvere le complicate formule che ne risultano dandole in pasto ai computer che, nel fare i calcoli, sono molto più veloci di noi.
Ma questo cosa c’entra con la Covid-19?
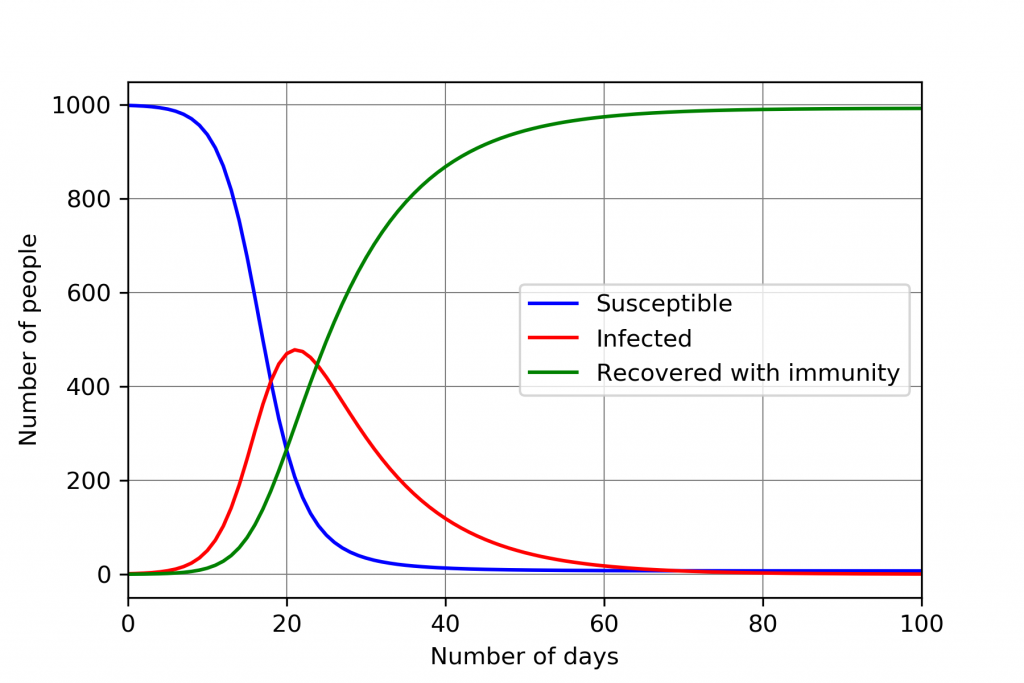
La Fisica dei Sistemi Complessi è proprio quella che si occupa di creare dei modelli anche per le epidemie, con il fine di trovare i modi migliori per contenerle che non prevedano l’estinzione della specie umana, né un irreparabile crollo economico. Si tratta di applicare i suddetti modelli matematici e i procedimenti della fisica a situazioni esterne. Lo studio della Population Dynamics (Dinamica della Popolazione) consiste proprio nel descrivere matematicamente e fisicamente le interazioni tra le persone e di conseguenza, per esempio, come si diffonde un virus. Uno dei modelli di base per descrivere le epidemie è il Modello SIR, che consiste nel dividere la popolazione in:
- Suscettibili (S): persone che possono essere infettate;
- Infetti (I): persone che possono contagiare altre;
- Rimossi (R): persone che non possono più essere infettate (decedute o guarite).
La situazione più semplice è quella per cui una persona viene contagiata quando entra in contatto con una infetta, cioè quando è presente un contatto tra S e I. Per descrivere matematicamente questo processo, ma anche per fare capire come funziona la modellizzazione, è necessario introdurre una piccola formula – non preoccupatevi, sarà l’unica -.
Numero di contagiati (S -> I) = (m ∙ β ∙ S ∙ I) / N
Dove m è una misura delle interazioni sociali tra le persone (è più grande, per esempio, in grandi città dove sono presenti molti eventi, è minore quando inizia la quarantena); β è la probabilità di essere contagiati (per esempio è diversa per ogni variante, diminuisce se si indossano le mascherine o se si è vaccinatɜ); S è il numero di suscettibili; I quello di infetti e N il numero totale di persone.
Adesso basta con il trattato di fisica. Quello che ci interessa è che siamo riusciti a descrivere una situazione reale con una formula matematica, seppur molto spartana – i modelli utilizzati nella realtà sono molto più complessi di così, ma l’idea di base è sempre la stessa -.
Il problema è che mentre S, I, N e β si ottengono dai dati, m è proprio uno di quei parametri matematici che sono molto difficili da identificare: d’altronde come si misura la socialità? In ogni caso, utilizzando programmi informatici, questo calcolo viene ripetuto in modo da ottenere il numero di contagiati giornalieri. Rappresentando questi risultati in un grafico si può vedere che, effettivamente, l’andamento è quello di una curva con diversi picchi che corrispondono alle varie ondate. Proprio come in uno di quei grafici che spesso vediamo in tv o sui giornali.
A questo punto abbiamo un modello che sembra descrivere bene i dati della realtà. Lɜ scienziatɜ lo utilizzano per due scopi: capire come modificare i parametri per non far diffondere il virus in maniera incontrollata e provare ad utilizzare il modello per prevedere lo sviluppo futuro.
Il primo obiettivo consiste nel ridurre il famoso parametro R che rappresenta il numero medio di persone infettate da una persona. È interessante notare che l’obiettivo non è semplicemente portarlo a 0 (che si otterrebbe semplicemente rimanendo tutti in quarantena abbastanza a lungo) ma mantenerlo intorno ad 1. In modo che l’epidemia sia sotto controllo e così che la vita delle persone possa continuare in maniera “normale”.
Per quanto riguarda le previsioni, invece, si procede in primis adattando il modello ottenuto ai dati reali, così da ottenere alcuni parametri caratteristici per la Covid-19 (ad esempio il β citato precedentemente), per poi ipotizzare eventuali scenari futuri in modo da scegliere quale sia quello migliore e provare a replicarlo nella realtà. E proprio qui intervengono con l’utilizzo di mascherine, il distanziamento, la quarantena e quant’altro: per ogni possibilità si prova a vedere come evolve il numero di contagiati e si sceglie la situazione migliore.
Sicuramente il passaggio dalla modellizzazione all’effettiva realizzazione delle misure ipotizzate dal Comitato Scientifico, non è semplice. Si tratta di scelte politiche che ovviamente non possono dipendere solo dalle ipotesi e dalle previsioni matematiche. Non perché queste non siano corrette, ma perché le decisioni governative, per fortuna, non dipendono solo dalla scienza, sebbene a tratti in Italia sia stato preso forse troppo sotto gamba il parere del Comitato Tecnico. Quello che è fondamentale capire, è che bisogna spesso affidarsi ad essa anche nella vita sociale, perché la scienza è fatta dalla società stessa, che la crea e la modifica. È proprio questo che la rende ancora più reale.